Fermionic compact stars

Compact stars achieve hydrostatic equilibirum very differently to main sequence stars. A white dwarf, for example, supports itself by the fermionic pressure exerted by electrons. White dwarfs are composed of degenerate electrons. And degenerate electrons obey the Pauli exclusion principle. To put it simply, fermions don’t like to be pushed together. But that’s exactly what gravity tries to do. And so, we have a balance - between the inward push of gravity and the outward push of the repulsive Fermi interaction.

The stabilisation against gravity is not limitless. As we move to heavier white dwarfs, a higher Fermi pressure is required to stabilise the star. Higher Fermi pressures imply higher Fermi velocities. This increase is only possible until we hit the cosmic speed limit. The speed of light. Once the electrons reach (close to) the speed of light, Fermi pressure can no longer support the star against gravity. This maximum limit upto which a white dwarf supports itself through the Fermi pressure of its constituent electrons is the famous Chandrasekhar limit .

The arguments made above can be generalised to any fermion, not just electrons. Theoretically, we can have a whole class of fermionic compact stars, characterised by the mass of the fermion that makes up the star. Such stars would have their own “Chandrasekhar”-type limiting mass. Through this work, we generated stars from different free fermion gas equations of state, and we were able to establish an inverse relationship between the limiting mass supported by the star, and the mass of the fermion making up the star. Linking a microscopic scale with a macroscopic one.

Further repulsive interactions, not connected to the fermionic nature of the star, can be introduced. In our work, we considered the causal limit of repulsive interactions - the Zeldovich interaction. In doing so, we were able to link a further scale to the two masses mentioned earlier. The scale of the mediator vector boson responsible for the interactions.

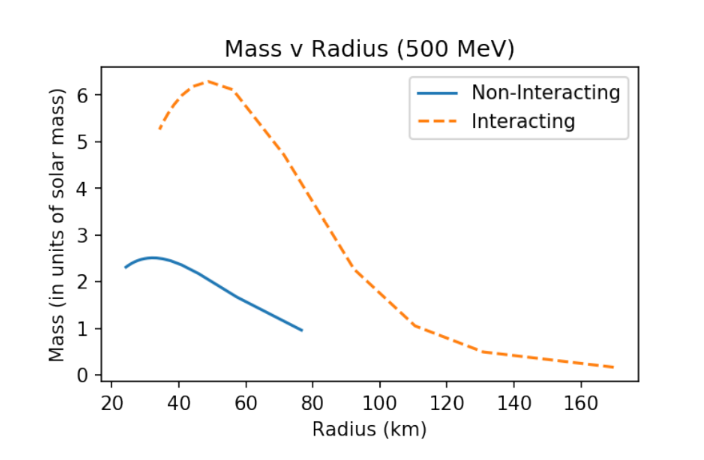
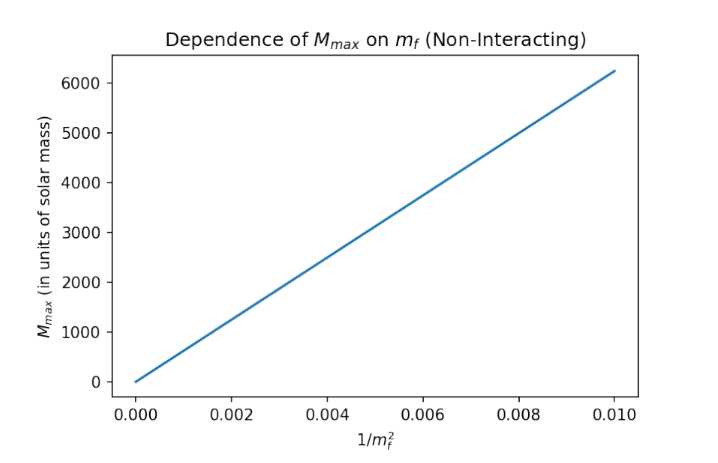
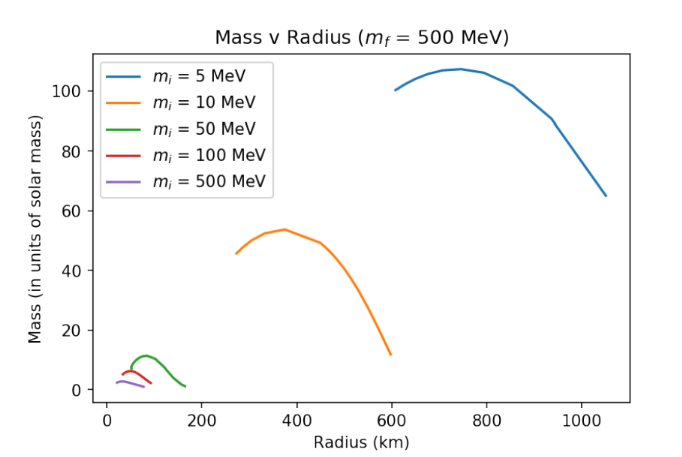
Some of the results from this line of work. On the left, a typical mass-radius curve for stars made of 500 MeV free fermion gas. The center picture establishes the link between the maximum "limiting" mass and the mass of the constituents of the star. The rightmost picture shows a variation of the mass-radius curve with different interaction strengths.

This is a brief description of work I did as part of my M.Sc. thesis, at NIT Tiruchirappalli, under the supervision of Dr. Somnath Mukhopadhyay. All figures used here are generated using Python 3.7.6.